布隆过滤器

发表于 2023-07-19 分类于 default 阅读次数：

简介

布隆过滤器有着广泛的应用，对于大量数据的“存不存在”的问题在空间上有明显优势，但是在判断存不存在是有一定的错误率(false positive)，也就是说，有可能把不属于这个集合的元素误认为属于这个集合(False Positive)，但不会把属于这个集合的元素误认为不属于这个集合(False Negative)。

布隆在 1970 年提出了布隆过滤器(Bloom Filter)，是一个很长的二进制向量(可以想象成一个序列)和一系列随机映射函数(hash function)。可用于判断一个元素是否在一个集合中，查询效率很高(1-N，最优能逼近于 1)。通常应用在一些需要快速判断某个元素是否属于集合，但是并不严格要求 100%正确的场合。

特点

优点: 占用空间小，查询快
缺点: 有误判，删除困难

专业术语

False Positive: 中文可以理解为“假阳性”，在这里表示，有可能把不属于这个集合的元素误认为属于这个集合
False Negative: 中文可以理解为“假阴性”，Bloom Filter 是不存在 false negatived 的，即不会把属于这个集合的元素误认为不属于这个集合(False Negative)

应用场景

网页爬虫对URL的去重: 避免爬取相同的 URL 地址；
反垃圾邮件: 假设邮件服务器通过发送方的邮件域或者 IP 地址对垃圾邮件进行过滤，那么就需要判断当前的邮件域或者 IP 地址是否处于黑名单之中。如果邮件服务器的通信邮件数量非常大(也可以认为数据量级上亿)，那么也可以使用 Bloom Filter 算法；
缓存击穿: 将已存在的缓存放到布隆中，当黑客访问不存在的缓存时迅速返回避免缓存及 DB 挂掉；
HTTP缓存服务器: 当本地局域网中的 PC 发起一条 HTTP 请求时，缓存服务器会先查看一下这个 URL 是否已经存在于缓存之中，如果存在的话就没有必要去原始的服务器拉取数据了(为了简单起见，我们假设数据没有发生变化)，这样既能节省流量，还能加快访问速度，以提高用户体验。
黑/白名单: 类似反垃圾邮件。
Bigtable: Google 著名的分布式数据库 Bigtable 使用了布隆过滤器来查找不存在的行或列，以减少磁盘查找的 IO 次数。
Squid: 网页代理缓存服务器在 cachedigests 中使用了也布隆过滤器。
Venti 文档存储系统: 也采用布隆过滤器来检测先前存储的数据。
SPIN 模型检测器: 也使用布隆过滤器在大规模验证问题时跟踪可达状态空间。
Chrome加速安全浏览: Google Chrome 浏览器使用了布隆过滤器加速安全浏览服务。
Key-Value系统: 在很多 Key-Value 系统中也使用了布隆过滤器来加快查询过程，如 Hbase，Accumulo，Leveldb，一般而言，Value 保存在磁盘中，访问磁盘需要花费大量时间，然而使用布隆过滤器可以快速判断某个 Key 对应的 Value 是否存在，因此可以避免很多不必要的磁盘 IO 操作，只是引入布隆过滤器会带来一定的内存消耗。
HTTP Proxy-Cache: 在 Internet Cache Protocol 中的 Proxy-Cache 很多都是使用 Bloom Filter 存储 URLs，除了高效的查询外，还能很方便得传输交换 Cache 信息。
网络应用: P2P 网络中查找资源操作，可以对每条网络通路保存 Bloom Filter，当命中时，则选择该通路访问。广播消息时，可以检测某个 IP 是否已发包。检测广播消息包的环路，将 Bloom Filter 保存在包里，每个节点将自己添加入 Bloom Filter。信息队列管理，使用 Counter Bloom Filter 管理信息流量。

布隆过滤器实现

Bloom Filter 在很多开源框架都有实现，例如:

Elasticsearch: org.elasticsearch.common.util.BloomFilter
guava: com.google.common.hash.BloomFilter
Hadoop: org.apache.hadoop.util.bloom.BloomFilter(基于 BitSet 实现)

以 BitSet 实现方式为例

创建一个 m 位 BitSet，先将所有位初始化为 0，然后选择 k 个不同的哈希函数。第 i 个哈希函数对字符串 str 哈希的结果记为 h(i，str)，且 h(i，str)的范围是 0 到 m-1 。

加入字符串过程

下面是每个字符串处理的过程，首先是将字符串 str“记录”到 BitSet 中的过程: 对于字符串 str，分别计算 h(1，str)，h(2，str)…… h(k，str)。然后将 BitSet 的第 h(1，str)、h(2，str)…… h(k，str) 位设为 1。

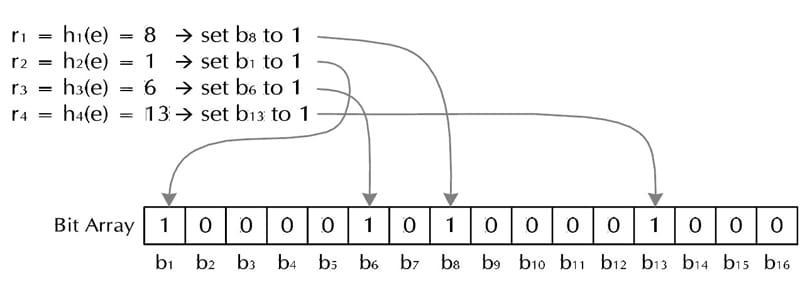
big-data-bloomfilter-加入过程

这样就将字符串 str 映射到 BitSet 中的 k 个二进制位了。

检查字符串是否存在的过程

下面是检查字符串 str 是否被 BitSet 记录过的过程: 对于字符串 str，分别计算 h(1，str)，h(2，str)…… h(k，str) 。然后检查 BitSet 的第 h(1，str)、h(2，str)…… h(k，str) 位是否为 1，若其中任何一位不为 1 则可以判定 str 一定没有被记录过。若全部位都是 1，则“认为”字符串 str 存在。若一个字符串对应的 Bit 不全为 1，则可以肯定该字符串一定没有被 Bloom Filter 记录过。(这是显然的，因为字符串被记录过，其对应的二进制位肯定全部被设为 1 了)

以 BitSet 实现方式的代码

package example.hash.bloomfliter;

import java.util.BitSet;

public class BloomFilter {
    /**
     * BitSet初始分配2^24个bit
     */
    private static final int DEFAULT_SIZE = 1 << 25;
    /**
     * 不同哈希函数的种子，一般应取质数
     */
    private static final int[] seeds = new int[]{5, 7, 11, 13, 31, 37, 61};
    private BitSet bits = new BitSet(DEFAULT_SIZE);
    /**
     * 哈希函数对象
     */
    private SimpleHash[] func = new SimpleHash[seeds.length];

    public BloomFilter() {
        for (int i = 0; i < seeds.length; i++) {
            func[i] = new SimpleHash(DEFAULT_SIZE, seeds[i]);
        }
    }

    /**
     * 将字符串标记到bits中
     */
    public void add(String value) {
        for (SimpleHash f : func) {
            bits.set(f.hash(value), true);
        }
    }

    /**
     * 判断字符串是否已经被bits标记
     */
    public boolean contains(String value) {
        if (value == null) {
            return false;
        }
        boolean ret = true;
        for (SimpleHash f : func) {
            ret = ret && bits.get(f.hash(value));
        }
        return ret;
    }

    /**
     * 哈希函数类
     */
    public static class SimpleHash {
        static final int MAXIMUM_CAPACITY = 1 << 30;

        private int cap;
        private int seed;

        public SimpleHash(int cap, int seed) {
            this.setCap(cap);
            this.seed = seed;
        }

        /**
         * 禁止子类重写
         */
        final void setCap(int cap) {
            int n = cap - 1;
            n |= n >>> 1;
            n |= n >>> 2;
            n |= n >>> 4;
            n |= n >>> 8;
            n |= n >>> 16;
            this.cap = (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
        }

        /**
         * hash函数，采用简单的加权和hash
         * 更多 hash 函数参考： {@link util.hash.HashUtils}
         */
        public int hash(String value) {
            int result = 0;
            for (int i = 0; i < value.length(); i++) {
                result = seed * result + value.charAt(i);
            }
            return (cap - 1) & result;
        }
    }
}

误报率 - False Positive Rate

误报率的产生

初始状态下，Bloom Filter 是一个 m 位的位数组，且数组被 0 所填充。同时，我们需要定义 k 个不同的 hash 函数，每一个 hash 函数都随机的将每一个输入元素映射到位数组中的一个位上。那么对于一个确定的输入，我们会得到 k 个索引。

插入元素: 经过 k 个 hash 函数的映射，我们会得到 k 个索引，我们把位数组中这 k 个位置全部置 1(不管其中的位之前是 0 还是 1)

查询元素: 输入元素经过 k 个 hash 函数的映射会得到 k 个索引，如果位数组中这 k 个索引任意一处是 0，那么就说明这个元素不在集合之中；如果元素处于集合之中，那么当插入元素的时候这 k 个位都是 1。但如果这 k 个索引处的位都是 1，被查询的元素就一定在集合之中吗? 答案是不一定，也就是说出现了 False Positive 的情况(但 Bloom Filter 不会出现 False Negative 的情况)

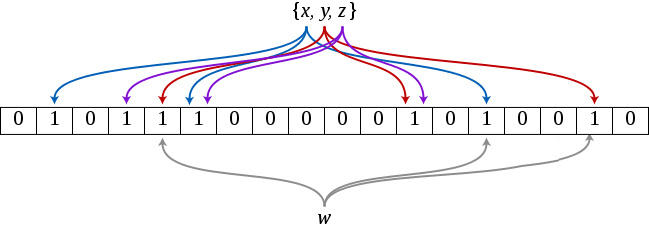
big-data-bloomfilter-1

在上图中，当插入 x、y、z 这三个元素之后，再来查询 w，会发现 w 不在集合之中，而如果 w 经过三个 hash 函数计算得出的结果所得索引处的位全是 1，那么 Bloom Filter 就会告诉你，w 在集合之中，实际上这里是误报，w 并不在集合之中。

误报率的计算

Bloom Filter 的误报率到底有多大? 下面在数学上进行一番推敲。假设 HASH 函数输出的索引值落在 m 位的数组上的每一位上都是等可能的。那么，对于一个给定的 HASH 函数，在进行某一个运算的时候，一个特定的位没有被设置为 1 的概率是

$1-\frac{1}{m}$

那么，对于所有的 k 个 HASH 函数，都没有把这个位设置为 1 的概率是

$(1-\frac{1}{m})^k$

如果我们已经插入了 n 个元素，那么对于一个给定的位，这个位仍然是 0 的概率是

$(1-\frac{1}{m})^{kn}$

那么插入 n 个元素之后，这个位是 1 的概率是

$1 - (1 - \frac{1}{m})^{kn}$

所以插入 n 个元素之后，第 n + 1 个元素经过 HASH 函数得到的 k 位都是 1 的概率是

$[1 - (1 - \frac{1}{m})^{kn}] ^ k$

根据常数 e 的定义，可以近似的表示为:

根据数学公式可以推理误判概率 $P_{error}$ 有如下关系：

$$
\begin{equation}\begin{split} P_{error} &= [1 - (1 - \frac{1}{m})^{kn}]^k \
&= [1 - (1 - \frac{1}{m})^{-m (- \frac{kn}{m})}]^k \
&\approx(1 - e ^ {- \frac{kn}{m}})^k \
\end{split}\end{equation}
$$

$m$ 是位数组的大小；
$n$ 是已经添加元素的数量；
$k$ 是哈希函数数量；
$e$ 数学常数，约等于 2.718281828。

减少误报率

通过上面的估计式也可以估计在给定的比特向量长度 m 以及插入次数 n 下使得误判率最小的哈希函数的个数, 考察关于 k 的函数 $f(k)$ (其中 n 和 m 是常数)

$$
f(k) = (1 - e ^ {- \frac{kn}{m}})^k
$$

由于 n 和 m 都是常数, 因此我们不妨将 $e ^ \frac{n}{m}$ 看做一个整体, 记为 t, 即 $t = e ^ \frac{n}{m}$, 于是

$$
f(k) = (1 - t^{-k})^k
$$

将上式两边取对数, 得

$$
ln f(k) = kln(1 - t^{-k})
$$

对上式两边求导, 有

$$
\frac{1}{f(k)}f’(k) = ln(1 - t ^ {-k}) + \frac{kt^{-k}lnt}{1 - t^{-k}}
$$

令上式等于 0, 解得

$$
t^{-k} = \frac{1}{2}
$$

即

$$
e ^ \frac{-kn}{m} = \frac{1}{2}
$$

于是,

$$
k = \frac{m}{n}ln2
$$

即当 $k = \frac{m}{n}ln2$ 时, 布隆过滤器的误判概率最低, 此时, 误判概率为

$$
P_{error} = (1 - \frac{1}{2}) ^k = 2 ^ {- ln2 \frac{m}{n}}
$$

最优的哈希函数个数和位数组的大小的推断：

布隆过滤器的原理很简单, 它的难点在于根据需要的误判概率确定过滤器的参数值 (比特向量长度 n, 哈希函数个数 k), 根据上一节的推导, 我们可以使用如下的结论:

在给定误判概率 P 下, k 应取 $- \frac{lnp}{ln2}$
在给定的元素数 n 和哈希函数个数 k 下, m 应取 $\frac{nk}{ln2}$

简介

特点